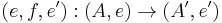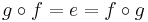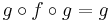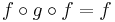Karoubi envelope

In mathematics the Karoubi envelope (or Cauchy completion or idempotent splitting) of a category C is a classification of the idempotents of C, by means of an auxiliary category. Taking the Karoubi envelope of a preadditive category gives a pseudo-abelian category, hence the construction is sometimes called the pseudo-abelian completion. It is named for the French mathematician Max Karoubi.

Given a category C, an idempotent of C is an endomorphism

$e: A \rightarrow A$

with

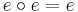$e\circ e = e$ .

An idempotent e: A → A is said to split if there is an object B and morphisms f: A → B, g : B → A such that e = g f and 1_B = f g.

The Karoubi envelope of C, sometimes written Split(C), is the category whose objects are pairs of the form (A, e) where A is an object of C and 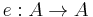$e�: A \rightarrow A$ is an idempotent of C, and whose morphisms are triples of the form

$(e, f, e^{\prime}): (A, e) \rightarrow (A^{\prime}, e^{\prime})$

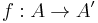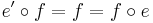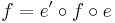where $f: A \rightarrow A^{\prime}$ is a morphism of C satisfying $e^{\prime} \circ f = f = f \circ e$ (or equivalently $f=e'\circ f\circ e$ ).

Composition in Split(C) is as in C, but the identity morphism on 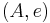$(A,e)$ in Split(C) is 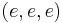$(e,e,e)$ , rather than the identity on $A$ .

The category C embeds fully and faithfully in Split(C). In Split(C) every idempotent splits, and Split(C) is the universal category with this property. The Karoubi envelope of a category C can therefore be considered as the "completion" of C which splits idempotents.

The Karoubi envelope of a category C can equivalently be defined as the full subcategory of 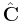$\hat{\mathbf{C}}$ (the presheaves over C) of retracts of representable functors. The category of presheaves on C is equivalent to the category of presheaves on Split(C).

Automorphisms in the Karoubi envelope

An automorphism in Split(C) is of the form 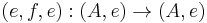$(e, f, e): (A, e) \rightarrow (A, e)$ , with inverse 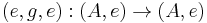$(e, g, e): (A, e) \rightarrow (A, e)$ satisfying:

$g \circ f = e = f \circ g$

$g \circ f \circ g = g$

$f \circ g \circ f = f$

If the first equation is relaxed to just have 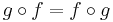$g \circ f = f \circ g$ , then f is a partial automorphism (with inverse g). A (partial) involution in Split(C) is a self-inverse (partial) automorphism.

Examples

If C has products, then given an isomorphism 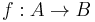$f: A \rightarrow B$ the mapping 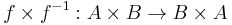$f \times f^{-1}: A \times B \rightarrow B \times A$ , composed with the canonical map 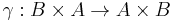$\gamma:B \times A \rightarrow A \times B$ of symmetry, is a partial involution.
If C is a triangulated category, the Karoubi envelope Split(C) can be endowed with the structure of a triangulated category such that the canonical functor C → Split(C) becomes a triangulated functor.^[1]
The Karoubi envelope is used in the construction of several categories of motives.
The Karoubi envelope construction takes semi-adjunctions to adjunctions.^[2] For this reason the Karoubi envelope is used in the study of models of the untyped lambda calculus. The Karoubi envelope of an extensional lambda model (a monoid, considered as a category) is cartesian closed.^[3]^[4]

References

^ Balmer & Schlichting 2001
^ Susumu Hayashi (1985). "Adjunction of Semifunctors: Categorical Structures in Non-extensional Lambda Calculus". Theoretical Computer Science 41: 95–104.
^ C.P.J. Koymans (1982). "Models of the lambda calculus". Information and Control 52: 306–332.
^ DS Scott (1980). "Relating theories of the lambda calculus". To HB Curry: Essays in Combinarory Logic.

Balmer, Paul; Schlichting, Marco (2001), "Idempotent completion of triangulated categories", Journal of Algebra 236 (2): 819–834, ISSN 0021-8693, http://www.math.ucla.edu/~balmer/research/Pubfile/IdempCompl.pdf